Python 数学、統計、機械学習：正規分布、確率密度関数

1.正規分布と確率密度関数

1.1 正規分布

正規分布は、数式(確率密度関数)で表現できる。

データの中心を示す平均(μ)とバラツキの大きさを示す標準偏差(σ)がわかれば、正規分布の形が決まる

平均値(μ)を中心に左右対称の釣り鐘型に分布
平均値、中央値、最頻値が一致
グラフで囲まれた部分が確率を表し、全体の合計が1となる
対応する面積を求めると確率が求まる

1.2 σ区間

確率密度関数の範囲について定積分(面積を求める)ことで、確率が求まる。

区間	範囲開始	範囲終了	正規分布の場合収まる確率
1σ 区間	平均(μ) – 標準偏差(σ)	平均(μ) + 標準偏差(σ)	約 68.27%
2σ 区間	平均(μ) – 2*標準偏差(σ)	平均(μ) + 2*標準偏差(σ)	約 95.45%
3σ 区間	平均(μ) – 3*標準偏差(σ)	平均(μ) + 3*標準偏差(σ)	約 99.73%

1.3 試してみる

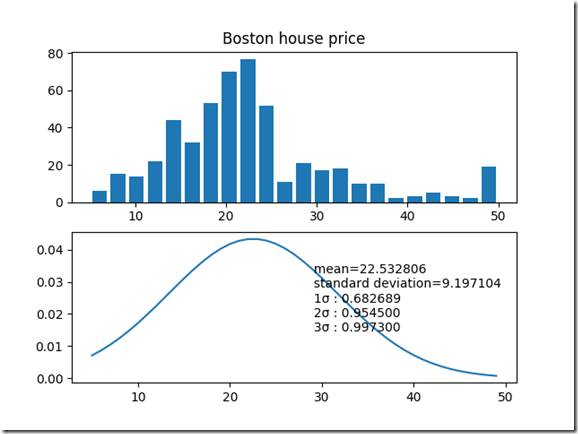
基本統計量の確認で使用したデータセットについて、正規分布と仮定しグラフを描画、また、σ区間の確率を定積分により計算。

from sklearn import datasets
import pandas as pd
import matplotlib.pyplot as plt
import math
import numpy as np
from scipy.stats import norm
from scipy import integrate
 
 
def normal_dist():
    """
    https://ja.wikipedia.org/wiki/%E7%A2%BA%E7%8E%87%E5%AF%86%E5%BA%A6%E9%96%A2%E6%95%B0
    https://mathtrain.jp/gaussdistribution
    https://mathtrain.jp/pmitsudo
    確率密度関数と正規分布
    :return:
    """
    boston = datasets.load_boston()
 
    df = pd.DataFrame(boston.target)
    df.columns = ['Price']
 
    x = df['Price']
    # CSVに出力
    # x.to_csv('~/work/house_price.csv')
 
    import pprint
    print(pprint.pprint(dir(x)))
 
    fig = plt.figure()
    # 2 * 1 の マトリックス 1番目のセルにグラフを描画
    ax = fig.add_subplot(2,1,1)
    ax.set_title('Boston house price')
    ax.hist(x, bins=int(round(math.sqrt(x.count()), 0)),
            rwidth=0.8, label='house price(x $1,000)')
 
    # 2 * 1 の マトリックス 2番目のセルにグラフを描画
    ax2 = fig.add_subplot(2, 1, 2)
    nx = np.arange(df.min(), df.max(), 1.0)
 
    # 確率密度関数(probability density function、PDF)を ラムダにラップし、
    # 関数にする(σ区間算出用)
    pdf = lambda px : norm.pdf(px, loc=x.mean(), scale=x.std())
 
    ax2.plot(nx, pdf(nx))
 
    # σ区間の確率を算出(定積分)
    sig = []
    for i in range(1, 4, 1):
        s, s1e = integrate.quad(pdf, x.mean() - (x.std() * i), x.mean() + (x.std() * i))
        sig.append(s)
 
    label = """
     mean={0:f}
     standard deviation={1:f}
     1σ : {2:f} 
     2σ : {3:f}
     3σ : {4:f}
     """.format(
        x.mean(),
        x.std(),
        sig[0], sig[1], sig[2])
 
    ax2.text(27, 0.01, label)
 
 
    plt.show()
 
if __name__ == "__main__":
    normal_dist()