Python 数学、統計、機械学習:散布図と相関分析(2) 単回帰分析
1.単回帰分析
- 単回帰分析とは、2つのデータ群を「原因」と「結果」でとらえたときに、その関係を「回帰直線」であらわすことのできる分析手法
- 単回帰式 y = ax + b を求めることで、値を予測できる
| 項目 | 内容 |
| 説明変数(x) | 原因系のデータ |
| 目的変数(y) | 結果系のデータ |
| 回帰係数(a) | 最小二乗法による傾き |
| 切片(b) | 最小二乗法によるy切片 |
| 決定係数 | 回帰式の精度判断基準として一般的に「単相関係数」を二乗した値が使われる。(決定係数、寄与率などと呼ばれる)0 から 1の値をとり、1に近いほど回帰式の精度がよい(xとyの関係が強い) |
2.試してみる
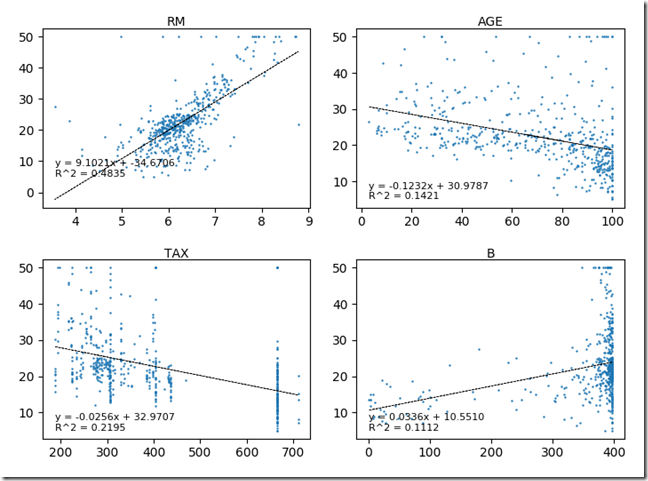
Python 数学、統計、機械学習:散布図と相関分析(1) で描いた散布図に回帰直線を重ねる
scikit-learn に含まれる、線形回帰モデルを利用する。
from sklearn import datasets
from sklearn import linear_model
import pandas as pd
import matplotlib.pyplot as plt
import math
def liner_regression(*feature_index):
"""
https://pythondatascience.plavox.info/scikit-learn/%E7%B7%9A%E5%BD%A2%E5%9B%9E%E5%B8%B0
:return:
"""
# 線形回帰予測クラス
lr = linear_model.LinearRegression()
boston = datasets.load_boston()
df_ex = pd.DataFrame(boston.data)
df_ex.columns = boston.feature_names
import pprint
print(pprint.pprint(df_ex))
df_res = pd.DataFrame(boston.target)
df_res.columns = ['Price']
y = df_res['Price']
fig = plt.figure()
cnt = len(feature_index)
cols = 1 if cnt == 1 else (2 if cnt < 6 else 4)
rows = math.ceil(cnt / cols)
idx = 1
for feature in feature_index:
x = df_ex[feature]
ax = fig.add_subplot(rows, cols, idx)
ax.set_title(feature, fontdict={'fontsize': 10}, pad=2)
ax.scatter(x, y, s=0.5)
mat_x = x.reshape((-1, 1))
mat_y = y.reshape((-1, 1))
# 予測モデルを作成
# y = ax + b
lr.fit(mat_x, mat_y)
# a:回帰係数
a = lr.coef_
# b:切片 (誤差)
b = lr.intercept_
# R^2:決定係数
r2 = lr.score(mat_x, mat_y)
# 予測を実行
predict = lr.predict(mat_x)
# 予測をプロット
ax.plot(x, predict, 'k--', lw=0.5)
label = "y = {0:.4f}x + {1:.4f}\nR^2 = {2:.4f}".format(a[0][0], b[0], r2)
ax.text(x.min(), y.min(), label, fontdict={'fontsize': 8})
idx = idx + 1
plt.tight_layout()
plt.show()
if __name__ == "__main__":
# liner_regression('CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT')
liner_regression('RM', 'AGE', 'TAX', 'B')
以下のようなエラーがでるので、指示に従って、x.reshape(-1, 1) としています。
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.
>>> import pandas as pd
>>> df = pd.DataFrame([1,2,3])
>>> df.columns = ['x']
>>> x = df['x']
x
0 1
1 2
2 3
Name: x, dtype: int64
>>> x.reshape((-1,1))
array([[1],
[2],
[3]])
LinearRegressionのAPIについて以下サイトから引用させてもらいます。
https://pythondatascience.plavox.info/scikit-learn/%E7%B7%9A%E5%BD%A2%E5%9B%9E%E5%B8%B0
sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False,
copy_X=True, n_jobs=1)
| パラメータ | 内容 |
| fit_intercept | False に設定すると切片を求める計算を含めない。目的変数が原点を必ず通る性質のデータを扱うときに利用。 (デフォルト値: True) |
| normalize | True に設定すると、説明変数を事前に正規化します。 (デフォルト値: False) |
| copy_X | メモリ内でデータを複製してから実行するかどうか。 (デフォルト値: True) |
| n_jobs | 計算に使うジョブの数。-1 に設定すると、すべての CPU を使って計算します。 (デフォルト値: 1) |
| 属性 | 内容 |
| coef_ | 偏回帰係数 |
| intercept_ | 切片 |
| メソッド | 内容 |
| fit(X, y[, sample_weight]) | 線形回帰モデルのあてはめを実行 |
| get_params([deep]) | 推定に用いたパラメータを取得 |
| predict(X) | 作成したモデルを利用して予測を実行 |
| score(X, y[, sample_weight]) | 決定係数 R2を出力 |
| set_params(**params) | パラメータを設定 |