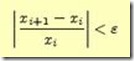一人読書会 「計算機プログラムの構造と解釈」 (7)
1.1.7 Newton 法による平方根
問題 1.7
1.ある繰返しから guess の変化に注目し、変化が予測値に比べ非常に小さくなった時点で止める手続きを設計する。これは小さい数、大きい数に対してうまく動くか?
(define (good-enough? guess pre-guess)
(< (abs (- guess pre-guess)) 0.001))
(define (average x y) (/ (+ x y) 2))
(define (improve guess x)
(average guess (/ x guess)))
(define (sqrt-itr guess x)
(if (good-enough? (improve guess x) guess)
(improve guess x)
(sqrt-itr (improve guess x)
x)))
(define (sqrt2 x) (sqrt-itr 1.0 x))
まず、単純に予測値の差が一定の値(0.001) 未満になったら、処理を終了するように good-enough? を書き換え、sqrt-itr の実装をそれにあわせて変更してみる。
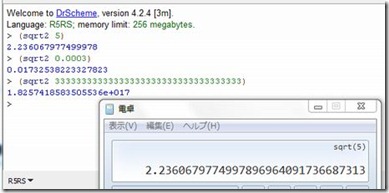
問題があった値に対して、確認してみる。
小さい値で、誤差が非常に大きくなってしまったり、大きい値で無限ループに陥ることはなくなった。
また、good-enough? での判定用定数を小さくすることで、精度もあがるようだ。
sqrt-itr で、improve が 2回 呼ばれるのが気になるが、まだ、Scheme で変数の使い方を知らないので、よしとしておく。
「これ以外にも計算の終了を決めることは可能なので、状況に応じて、計算の打ち切り方法を決めればよい。」 とのこと。
大きい数、小さい数に対しても、うまく動く。・・・ と思うんだけどなぁ。「それなりにうまく動く」か?