一人読書会 「計算機プログラムの構造と解釈」 (6)
1.1.7 Newton 法による平方根
問題 1.7
さて、ようやく問題の内容自体を理解できる準備が整ったので、考えてみる。問題の概要。
(define (square x) (* x x))
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
(define (average x y) (/ (+ x y) 2))
(define (improve guess x)
(average guess (/ x guess)))
(define (sqrt-itr guess x)
(if (good-enough? guess x)
guess
(sqrt-itr (improve guess x)
x)))
(define (sqrt2 x) (sqrt-itr 1.0 x))
まず、動きを検証するのに、デバッグ文を仕込んだりしたいのだが、Scheme でどうするのかさっぱりわからないので、Python に上記を移植してみる。
# -*-encoding:utf-8-*-
'''
http://ja.wikipedia.org/wiki/IEEE_754
'''
from decimal import *
def init_env():
'''環境の設定'''
global use_decimal # Decimal を利用するか
global judge # 計算打ち切り判定
global initial_guess # 推測初期値
use_decimal = True
getcontext().prec = 6
judge = dcm('0.00001')
initial_guess = '1.0'
def dcm(x):
'''数値を扱う型を切り替える float, decimal'''
if use_decimal:
return Decimal(x)
else:
return float(x)
def square(x):
return dcm(x) * dcm(x)
def good_enough(guess ,x):
g2 = square(guess)
v = g2 - dcm(x)
if v < dcm('0'):
v = v * dcm('-1')
print '*** %s - %s = %s ***' % (g2, dcm(x), v)
return v < judge
def avarage(x, y):
return (dcm(x) + dcm(y)) / dcm('2')
def improve(guess, x):
av = avarage((dcm(x) / dcm(guess)), guess)
print av
return av
def sqrt_itr(guess, x):
if good_enough(guess, x):
return dcm(guess)
else:
return sqrt_itr(improve(guess, x), x)
def sqrt2(x):
init_env()
return sqrt_itr(initial_guess, x)
if __name__ == '__main__':
target = '0.00003'
print sqrt2(target)
init_env 関数に、設定を行うようにしている。
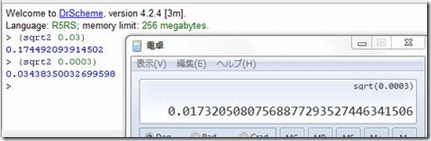
1.good-enough? テストは、非常に小さい数の平方根をとるときには効果的ではない。
good-enough? テストは、誤差が 0.001 という定数 以下になったら、計算を打ち切るようになっている。
まず、定数になっていることから、直感的に非常に小さい値の場合、誤差の割合が相対的に大きくなると思われる。
また、判定基準が 0.001 となっているが、この値を比較するのは、平方根をとる前(とろうとしている)値のため、求める値が1以下の値の場合平方根もさらに小さな値になり、判定基準の値、0.001 が、求める値に対して相対的にかなり大きくなってしまう。
use_decimal = True
def init_env():
(略)
use_decimal = True # Decimal を使う
getcontext().prec = 6 # Decimal の有効桁数を 6桁に
judge = dcm('0.00001') # 0.001 より精度をあげる
initial_guess = '1.0'
if __name__ == '__main__':
target = '0.0003'
print sqrt2(target)
上記 Python の init_env の設定を上記にして検証してみる。
*** 予測値 – 平方根をとる値 = good-enough? の判定値
*** 1.00 – 0.0003 = 0.9997 ***
0.50015
*** 0.250150 – 0.0003 = 0.249850 ***
0.250375
*** 0.0626876 – 0.0003 = 0.0623876 ***
0.125786
*** 0.0158221 – 0.0003 = 0.0155221 ***
0.0640855
*** 0.00410695 – 0.0003 = 0.00380695 ***
0.0343834
*** 0.00118222 – 0.0003 = 0.00088222 *** ← ここで判定OKとなってしまう。
0.0215542
*** 0.000464584 – 0.0003 = 0.000164584 ***
0.0177363
*** 0.000314576 – 0.0003 = 0.000014576 ***
0.0173254
*** 0.000300169 – 0.0003 = 1.69E-7 ***
0.0173254
かなり(0.001より)精度が悪い結果になってしまっている。
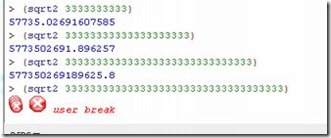
2.限られた精度で実行される場合、非常に大きい数にも不適切。
翻って、非常に大きい値の場合。おそらく、内部数値表現の精度によって、対象が大きい値だと 0.001 という精度自体を保てないためだと思われるが、実際どうなのか確認してみる。
どんどん値を大きくしていくと、結果がかえってこなくなった。
Python で確認してみる。
use_decimal = True
def init_env():
(略)
use_decimal = False # Decimal は使わない(floatとなる)
judge = dcm('0.001')
initial_guess = '1.0'
if __name__ == '__main__':
target = '33333333333333333333333333333333333'
print sqrt2(target)
やはり、ある程度以上は、予測値が近づかず、変化しないため、無限ループになってしまっているようだ。
(略)
*** 3.33333333333e+34 – 3.33333333333e+34 = 4.61168601843e+18 ***
1.82574185835e+17
*** 3.33333333333e+34 – 3.33333333333e+34 = 4.61168601843e+18 ***
1.82574185835e+17
(同じ処理の繰り返し・・・)
Traceback (most recent call last):
File “C:\test.py”, line 50, in <module>
print sqrt2(target)
File “C:\test.py”, line 46, in sqrt2
return sqrt_itr(initial_guess, x)
File “C:\test.py”, line 43, in sqrt_itr
(略)
RuntimeError: maximum recursion depth exceeded while calling a Python object
Python で、 計算に利用する数値データ型を、float から Decimal に変えて、十分に桁数をとれば、処理は完了するので、あくまで 内部数値データ型の問題だろう。