Python 数学、統計、機械学習:重回帰分析
1.重回帰分析
Bostonデータセットの各項目の内容を説明変数として、scikit-learn を用いて線形回帰モデルを作成、重回帰分析を行ってみる。
from sklearn import datasets
import pandas as pd
import statsmodels.formula.api as smf
import matplotlib.pyplot as plt
import numpy as np
def multi_regression(*feature_index):
"""
重回帰分析
https://pythondatascience.plavox.info/scikit-learn/%E7%B7%9A%E5%BD%A2%E5%9B%9E%E5%B8%B0
https://pythondatascience.plavox.info/matplotlib/%E6%A3%92%E3%82%B0%E3%83%A9%E3%83%95
:return:
"""
boston = datasets.load_boston()
df = pd.DataFrame(boston.data)
df.columns = boston.feature_names
df['PRICE'] = pd.DataFrame(boston.target)
x = df.loc[:, ['{0}'.format(x) for x in feature_index]]
y = df['PRICE']
model = smf.OLS(y, x)
result = model.fit()
print(result.summary())
# numpy sort
# https://qiita.com/supersaiakujin/items/c580f2aae90818150b35
desc_idx = np.argsort(result.tvalues.values)[::-1]
labels = []
values = []
for idx in desc_idx:
labels.append(feature_index[idx])
values.append(result.tvalues.values[idx])
plt.bar(labels, values)
plt.legend(title="r^2(adj) = {0:.6}".format(result.rsquared_adj))
plt.show()
if __name__ == "__main__":
multi_regression('CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT')
# multi_regression('RM', 'AGE', 'TAX', 'B')
分析結果について、summary() メソッドを呼び出すことで、以下の結果表が得られる。
OLS Regression Results
==============================================================================
Dep. Variable: PRICE R-squared: 0.959
Model: OLS Adj. R-squared: 0.958
Method: Least Squares F-statistic: 891.1
Date: Mon, 04 Jun 2018 Prob (F-statistic): 0.00
Time: 22:53:10 Log-Likelihood: -1523.8
No. Observations: 506 AIC: 3074.
Df Residuals: 493 BIC: 3129.
Df Model: 13
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
CRIM -0.0916 0.034 -2.675 0.008 -0.159 -0.024
ZN 0.0487 0.014 3.379 0.001 0.020 0.077
INDUS -0.0038 0.064 -0.059 0.953 -0.130 0.123
CHAS 2.8564 0.904 3.160 0.002 1.080 4.633
NOX -2.8808 3.359 -0.858 0.392 -9.481 3.720
RM 5.9252 0.309 19.168 0.000 5.318 6.533
AGE -0.0072 0.014 -0.523 0.601 -0.034 0.020
DIS -0.9680 0.196 -4.947 0.000 -1.352 -0.584
RAD 0.1704 0.067 2.554 0.011 0.039 0.302
TAX -0.0094 0.004 -2.393 0.017 -0.017 -0.002
PTRATIO -0.3924 0.110 -3.571 0.000 -0.608 -0.177
B 0.0150 0.003 5.561 0.000 0.010 0.020
LSTAT -0.4170 0.051 -8.214 0.000 -0.517 -0.317
==============================================================================
Omnibus: 204.050 Durbin-Watson: 0.999
Prob(Omnibus): 0.000 Jarque-Bera (JB): 1372.527
Skew: 1.609 Prob(JB): 9.11e-299
Kurtosis: 10.399 Cond. No. 8.50e+03
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 8.5e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
No handles with labels found to put in legend.
いろいろ警告が出ていますが、結果の見方を知りたい。
説明変数の各項目については、Bostonデータセットを引き続き使用
| 項目 | 内容 |
| 最小二乗回帰(OLS : Ordinary Least Squares regression) | 分析モデルとして最小二乗法を使用 |
| 回帰係数(ceof) | 回帰係数は単位の影響を受けるため、影響度の指標としては利用できない |
| 標準誤差(std err) | 平均からのバラツキを示す指標、分散の正の平方根 |
| t値(t) | 目的変数に対するそれぞれの説明変数の影響度を表す。回帰係数は単位の影響を受け、影響度の指標に利用できないため、回帰係数を標準誤差で除し単位の影響を受けないt値を利用する。t値の絶対値が大きいほど、影響度の強い説明変数といえる |
| P-値 | p値 は、全く効果がない場合(係数=0)に、分析結果として出る係数の値が、A以上になる確率を表す。 |
| 下限97.5% | 97.5%の信頼区間下限。 |
| 上限97.5% | 97.5%の信頼区間上限 |
| 重決定 R2(R-squared) | 寄与率または決定係数と呼ばれ、回帰式全体の精度を表す。1に近いほど制度が高いといえる。 |
| 補正 R2(Adj R-squared) | 自由度調整済み決定係数 |
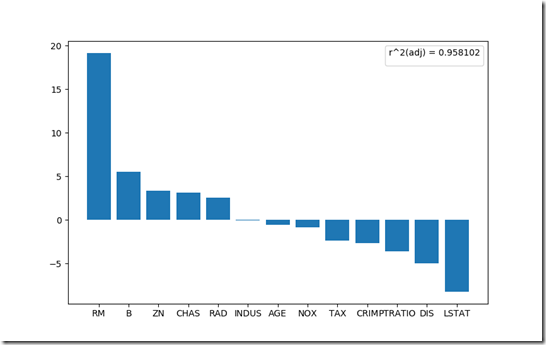
t値を降順にソートして棒グラフにプロット。
住宅価格に影響を与えている変数を分析できる。