一人読書会 「計算機プログラムの構造と解釈」 (4)
1.1.7 Newton 法による平方根
Newton法 により平方根を求める手続きを実装する。
問題 1.7
平方根の計算で使った good-enough? テストは非常に小さい値の平方根をとるときには効果的ではない。また限られた精度において非常に大きい数にも不適切である。それぞれどのようにテストが失敗するか?また、変化が予測値にくらべ非常に小さくなった時に終了する手続きを設計せよ。
まず、残念ながら、Newton 法 を知らないので、今年の目標は数学の勉強をすることなので、読み流さずにWikipediaで調べることとする。
重ねて残念ながら、Wikipedia の説明では、知識不足で、わかったような、わからないような。
偶然、所有している本「微分・積分のしくみ」に、ニュートン近似として、丁寧な説明があったので、まずそちらを参考にして、Newton法による平方根の近似とはどんなものかの理解を試みる。
たとえば、√5 の値を調べるとする。
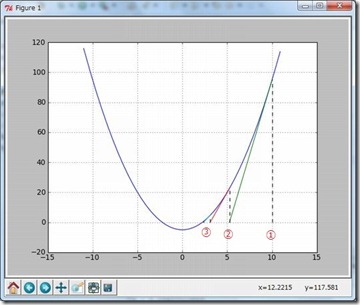
2次関数のグラフを書く
まず、上の図の2次関数のグラフは、y = x^2 – 5 のグラフ。
√5 を 満たすx、 x = √5 は、 x^2 = 5 であり、 x^2 – 5 = 0 となる。
Python で、
- exp = lambda x : x**2 - 5
と定義してみる。
適当な開始位置を決める
求めたいのは、上記の2次関数のグラフで、y=0 となるときの x の値。グラフを見ると、0 ~ 5 の間にあるので、とりあえず開始位置を x = 10 としてみる。すると、x = 10 の場合、y = 95 に値が定まる。(上図①)
接線を求め、x軸との交点を求める
y = x^2 – 5 のグラフ上の、上記で決めた (10, 95) での接線が、x1 で、y = 0 となる接線の方程式を求める。
y = f(x) = x^2 – 5 を 微分すると f'(x) = 2x で、f'(10) = 20 が 接線の傾きになる。
とすると、
接線の方程式 : y – f(a) = f'(a)(x – a)
y – 95 = 20x – 200
y = 20x – 105
( y = 20x + b 、 95 = 200 + b 、 b = -105 )
この接線が、y = 0 となるのは、x = 5.25 となる (上図②)
これで、みてわかるように、最初の値、x = 10 より、y = x^2 – 5 の x軸との交点により近づいた。
ここで取得した値、5.25 を初期値として、上記の処理を繰り返すことで、√5 の値に近似していく。
というのが ニュートン近似だと。
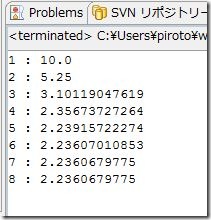
計算結果を出力してみる。
ようするに、n をどんどん増やしていくと、徐々に近づいていっているのがわかる。とりあえず、富士山麓に鸚鵡が鳴く条件は満たした。
グラフのコードなど
Python で グラフを書くための準備については、以下を参照
Python で グラフをかけるようにしとくと、こういった勉強の時に役立つなぁ。と。簡単にかけるし。Python イイ!
/tips/wiki.cgi?page=Python+NumPy
/tips/wiki.cgi?page=Python+matplotlib
上記のコード
- # -*- encoding:utf-8 -*-
- from pylab import *
- from numpy import *
- from numpy.ma.core import arange
- # 二次関数 f(x) y = x^2 - 5
- exp = lambda x : x**2 - 5
- # 二次関数の微分 f'(x) y = x^2 - 5
- expd = lambda x : 2 * x
- def f1(x_range, intarval):
- '''
- 関数expに対して、xの値 x_range[0] ~ x_range[1] 間隔 intarval に対応する y を取得
- '''
- x = arange(x_range[0], x_range[1], intarval)
- y = [exp(tx) for tx in x]
- return (x, y)
- if __name__ == '__main__':
- grid(True)
- # 二次関数のグラフを書く
- (x, y) = f1((-11.0, 11.0),0.1)
- plot(x, y)
- # 適当な値を設定
- tmp_x2 = 10.0
- repeat = 5
- for i in range(repeat):
- print '%d : %s' % (i+1, tmp_x2)
- tmp_x1 = tmp_x2
- x1 = (tmp_x2, tmp_x1)
- y1 = (0, exp(tmp_x1))
- plot(x1, y1, 'k--')
- tmp_x2 = tmp_x1 - (exp(tmp_x1) / expd(tmp_x1))
- x1 = (tmp_x2, tmp_x1)
- y1 = (0, exp(tmp_x1))
- plot(x1, y1)
- show()
ようやく、問題に取りかかる準備ができた。
このペースだと読了するのに1年ではきかんな~。