| ページ一覧 | ブログ | twitter |　 書式 | 書式(表) |

MyMemoWiki

「機械学習」の版間の差分

提供: MyMemoWiki
ナビゲーションに移動 検索に移動
 
(同じ利用者による、間の101版が非表示)
1行目: 1行目:
 +
| [[TensorFlow]] | [[Docker]] | [[Ubuntu]] | [[数学]] | [[統計]] | [[ベイズ統計]] | [[データ解析]] | [[R]] | [[Python NumPy]] |
 
==機械学習==
 
==機械学習==
−
{{amazon|4839964742}}
+
{{amazon|4295010073}}
 +
*https://github.com/rasbt/python-machine-learning-book-3rd-edition
 +
 
 +
==3種類の機械学習==
 +
===1.教師あり学習(supervised learning)===
 +
----
 +
*ラベル付された'''訓練データ'(training data)''からモデルを学習し、未知のデータを予測できるようにする
 +
*離散値のクラスラベルを持つ教師あり学習は'''分類'(classification)''とも呼ばれる
 +
*教師あり学習の'''回帰(regression)'''サブフィールドの場合、出力信号は連続値となる
 +
====クラスラベルの予測(分類)====
 +
----
 +
*分類は新しいインスタンスを対象としてクラスラベルを予測することが目標
 +
*インスタンスの'''所属関係(group membership)'''として解釈できる
 +
*メールスパムフィルタは、'''二値分類(binary classification)'''の典型例
 +
**'''’陰性クラス(negative class)'''と'''陽性クラス(positive class)'''を区別する'''決定境界(decision　boundary)'''を学習すれば分類できる
 +
*'''多クラス分類(multiclass classification)'''の典型例として手書き文字認識が挙げられる
 +
====連続値を予測(回帰)====
 +
----
 +
*連続値を予測する'''回帰分析(regression　analysis)'''では、複数の'''予測変数(predictor　variable)'''と連続値の'''応答変数(response　variable)'''が与えられれ結果を予測できるようにそれらの関係を探る
 +
*予測に使われる変数は'''説明変数(explanatory variable)'''、予測したい変数は'''成果指標(outcome)'''
 +
*機械学習では予測変数は一般的に'''特徴量(feature)'''と呼び、応答変数を'''目的変数(target variable)'''と呼ぶ
 +
===2.強化学習(reinforcement learning)===
 +
----
 +
*強化学習の目的は環境とのやり取りに基づいて性能を改善するシステムを構築することで、そうしたシステムは'''エージェント(agent)'''
 +
*環境の現在状態情報には、いわゆる'''報酬(reward)'''信号が含まれるため、教師あり学習に関連する分野とみなされる
 +
*チェスチェンジの例では、環境(チェス番)の状況に応じコマの動きを決定し、ゲームの勝ち負けが報酬tなる
 +
 
 +
===3.教師なし学習===
 +
----
 +
*教師なし学習では、エージェントの特定の行動に対して、正解ではなく、'''報酬(rewarｄ)'''の度合いを定義する
 +
*ラベル付されていないデータや'''構造が不明'''なデータを扱うことになる
 +
*目的変数や報酬関数がなくても、データの構造を調べて意味のある構造を取り出すことができる
 +
====クラスタリング(clustering)====
 +
----
 +
*大量の情報を意味のあるグループ(クラスタ)として構造化できる探索的データ解析手法
 +
*'''教師なし分類(unsupervised　classification)'''とも呼ぼれる
 +
*例として、マーケティング担当者が顧客の関心に基づいて顧客集団を発見できる
 +
====データ圧縮のための次元削減====
 +
----
 +
*'''次元削減(dimensionally reduction / dimension resuction)'''というサブフィールド
 +
*教師なし次元削減は特徴量の前処理においてよく使用されるアプローチの一つ
 +
==機械学習システム構築==
 +
===1.前処理：データ整形===
 +
----
 +
*生データが機械学習アルゴリズム性能最適化に適した形で提供されることはまずないため、データ'''前処理((preprocessing)'''が最も重要な処理の一つとなる
 +
===2.予測モデルの訓練と選択===
 +
----
 +
*'''交差検証(cross-validation)'''では、モデルの'''汎化性能(generalization　performance)'''を想定するために、データセットを訓練用と検証用に分割する
 +
*'''ハイパーパラメータ最適化(hypeparameter　optimization)'''はデータから学習されるものではなく、モデルの「ツマミ」を回すのに相当し、回すことでモデルの性能を向上させることができる
 +
===3.モデルの評価と未知のインスタンスの予測===
 +
----
 +
*訓練データセットにうまく適合するモデルを選択した後は、いわゆる汎化誤差(学習時に使わなかったデータに対する予測値と正解の差)を評価できる
 +
*性能に納得がいけば、このモデルを使って将来データを予測できる
 +
==分類問題==
 +
*散布図
 +
[[File:perceptron01.png|300px]]
 +
===[https://ja.wikipedia.org/wiki/%E7%B7%9A%E5%BD%A2%E5%88%86%E9%A1%9E%E5%99%A8#:~:text=%E7%B7%9A%E5%BD%A2%E5%88%86%E9%A1%9E%E5%99%A8%EF%BC%88%E8%8B%B1%3A%20Linear,%E3%81%93%E3%81%A8%E3%82%92%E7%9B%AE%E7%9A%84%E3%81%A8%E3%81%99%E3%82%8B%E3%80%82 線形分類器]===
 +
----
 +
*特徴の線形結合の値に基づいて分類を行う確率的分類器である。機械学習において、分類は項目群を特徴値に基づいてグループに分類することを目的とする
 +
*パーセプトロンアルゴリズムは、完全な線形分類が不可能なデータセットでは決して収束しないため、一般に実務データ解析で推奨されない
 +
 
 +
===[https://ja.wikipedia.org/wiki/%E3%83%91%E3%83%BC%E3%82%BB%E3%83%97%E3%83%88%E3%83%AD%E3%83%B3 パーセプトロン]===
 +
----
 +
パーセプトロンモデルは、脳内の1つのニューロンの働き、発火するかしないか、を模倣
 +
#　重みを0または値の小さな乱数で初期化
 +
#　訓練データごとに次の手順を実行
 +
##　出力値を計算
 +
##　重みを更新
 +
[[File:perceptron02.png|300px]] [[File:perceptron03.png|300px]]
 +
===ADALINE===
 +
----
 +
*パーセプトロンアルゴリズムの改良と見なすことができる。違いは重みの更新方法にある。
 +
*パーセプトロンのような単位ステップ関数ではなく、線形活性化関数に基づいて重みを更新する
 +
[[File:adaline02.png|300px]] [[File:adaline01.png|300px]]
 +
 
 +
===ロジスティック回帰(logistic regression)===
 +
----
 +
*線形分類問題と二値分類問題に対する単純ながら強力なアルゴリズムの一つ
 +
*名前とは裏腹に怪奇ではなく分類のためのモデル
 +
*非常に実装しやすく、線形分離可能なクラスでは非常に性能が良い
 +
*産業界において最も広く使われている分類アルゴリズムの1つ
 +
====オッズ比====
 +
*確率<math>p</math>の場合、事象の起こりやすさをオッズ比（odds ratio)として、<math>\tfrac{p}{(1-p)}</math>と書くことができる
 +
*<math>p</math>は、正事象(positive event 予測したい事象)を表す
 +
*オッズの対数を取ったものを、[https://mathwords.net/logitkansu ロジット(logit)関数]という。
 +
<math>
 +
logit(p) = log\frac{p}{(1 - p)}
 +
</math>
 +
*ロジット関数の逆関数は、ロジスティックシグモイド(logistic sigmoid)関数とも呼ばれる。
 +
<math>
 +
\phi(z) = \frac{1}{(1 + e^{-z})}
 +
</math>
 +
 
 +
==scikit-learn==
 +
===インストール===
 +
----
 +
<pre>
 +
$ pip install scikit-learn
 +
</pre>
 +
*Irisデータセットは、scikit-learnに組み込まれている
 +
<pre>
 +
>>> from sklearn import datasets
 +
>>> import numpy as np
 +
>>> iris = datasets.load_iris()
 +
>>> X = iris.data[:, [2,3]]
 +
>>> y = iris.target
 +
>>> print('Class labels:', np.unique(y))
 +
Class labels: [0 1 2]
 +
</pre>
 +
 
 +
==・・・・・・・・・・・・・・・・・==
 +
 
 
===基礎===
 
===基礎===
 
----
 
----
47行目: 159行目:
 
*環境が行動によりどう反応するかを観察することで収集される情報を訓練する
 
*環境が行動によりどう反応するかを観察することで収集される情報を訓練する
 
*どのような行動の組み合わせが最も有利な結果をもたらすかを知るため
 
*どのような行動の組み合わせが最も有利な結果をもたらすかを知るため
 +
 
===[[アルゴリズム]]===
 
===[[アルゴリズム]]===
 
{| class="wikitable"
 
{| class="wikitable"
106行目: 219行目:
 
|  
 
|  
 
|-
 
|-
 +
|}
 +
 +
==線形回帰==
 +
===バリアンスとバイアス===
 +
*[https://www.atmarkit.co.jp/ait/articles/2009/09/news025.html バイアスとバリアンス（偏りと分散）のトレードオフ（Bias-Variance Tradeoff）とは？]
 +
*'''バイアス'''（偏り：Bias）とは、予測値と真の値（＝正解値）とのズレ（つまり「偏り誤差：Bias error」）を指す
 +
**バイアス（偏り誤差）が大きすぎる場合、そのモデルは入力と出力の関係性を正確に表現できていない（＝訓練データでさえも正確に予測できない）といえる。いわゆる「学習不足（＝過少適合：under-fitting）」の状態
 +
*'''バリアンス'''（分散：Variance）とは、予測値の広がり（つまり「ばらつき誤差：Variance error」）を指す。この予測誤差は、訓練データの揺らぎから生じる
 +
**バリアンス（ばらつき誤差）が大きすぎる場合、そのモデルは訓練データのノイズまで学習してしまっている（＝テストデータなど未知のデータでは正確に予測できない）。いわゆる「過学習（＝過剰適合：over-fitting）」の状態
  
−
|}
+
[[TensorFlow]]
 +
<pre>
 +
import matplotlib
 +
matplotlib.use("WebAgg")
 +
import numpy as np
 +
import matplotlib.pyplot as plt
 +
 
 +
x_train = np.linspace(-1, 1, 101)
 +
y_train = 2 * x_train + np.random.randn(*x_train.shape) * 0.33
 +
 
 +
plt.scatter(x_train, y_train)
 +
plt.show()
 +
</pre>
 +
[[File:ml_regression.png|400px]]
 +
 
 +
==[[TensorFlow]]==
 +
*[[TensorFlow]]
 +
 
 +
 
 +
 
 +
==Irisデータセット==
 +
<pre>
 +
import pandas as pd
 +
import numpy as np
 +
import matplotlib.pyplot as plt
 +
 
 +
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
 +
df = pd.read_csv(url, header=None, encoding='utf-8')
 +
result = df.tail()
 +
print(result)
  
−
==[https://www.tensorflow.org/?hl=ja TensorFlow]==
+
y = df.iloc[0:100, 4].values
−
*Googleが公開した機械学習フレームワーク
+
y = np.where(y == 'Iris-secosa', -1, 1)
−
*便利な[[Python]] APIと比較すると劣るがC++ APIを備える
+
X = df.iloc[0:100, [0, 2]].values
−
*すべての[[数学]]は抽象化される
+
plt.scatter(X[:50,0], X[:50,1], color='red', marker='o', label='setosa')
−
*[https://www.tensorflow.org/tensorboard/get_started?hl=ja TensorBoard]というインタラクティブな可視化環境
+
plt.scatter(X[50:100,0], X[50:100, 1], color='blue', marker='x', label='versicolor')
−
===[https://www.tensorflow.org/install?hl=ja インストール]===
+
plt.xlabel('sepal length[cm]')
−
----
+
plt.ylabel('petal length[cm]')
 +
plt.legend(loc='upper left')
 +
plt.savefig('03.sample.png') # 画像を保存
 +
plt.show()
 +
</pre>
 +
[[File:iris_df01.png|500px]]

2021年8月31日 (火) 12:42時点における最新版

| TensorFlow | Docker | Ubuntu | 数学 | 統計 | ベイズ統計 | データ解析 | R | Python NumPy |

機械学習

4295010073.09.MZZZZZZZ.jpg link

3種類の機械学習

1.教師あり学習(supervised learning)

  • ラベル付された'訓練データ'(training data)からモデルを学習し、未知のデータを予測できるようにする
  • 離散値のクラスラベルを持つ教師あり学習は'分類'(classification)とも呼ばれる
  • 教師あり学習の回帰(regression)サブフィールドの場合、出力信号は連続値となる

クラスラベルの予測(分類)

  • 分類は新しいインスタンスを対象としてクラスラベルを予測することが目標
  • インスタンスの所属関係(group membership)として解釈できる
  • メールスパムフィルタは、二値分類(binary classification)の典型例
    • ’陰性クラス(negative class)と陽性クラス(positive class)を区別する決定境界(decision　boundary)を学習すれば分類できる
  • 多クラス分類(multiclass classification)の典型例として手書き文字認識が挙げられる

連続値を予測(回帰)

  • 連続値を予測する回帰分析(regression　analysis)では、複数の予測変数(predictor　variable)と連続値の応答変数(response　variable)が与えられれ結果を予測できるようにそれらの関係を探る
  • 予測に使われる変数は説明変数(explanatory variable)、予測したい変数は成果指標(outcome)
  • 機械学習では予測変数は一般的に特徴量(feature)と呼び、応答変数を目的変数(target variable)と呼ぶ

2.強化学習(reinforcement learning)

  • 強化学習の目的は環境とのやり取りに基づいて性能を改善するシステムを構築することで、そうしたシステムはエージェント(agent)
  • 環境の現在状態情報には、いわゆる報酬(reward)信号が含まれるため、教師あり学習に関連する分野とみなされる
  • チェスチェンジの例では、環境(チェス番)の状況に応じコマの動きを決定し、ゲームの勝ち負けが報酬tなる

3.教師なし学習

  • 教師なし学習では、エージェントの特定の行動に対して、正解ではなく、報酬(rewarｄ)の度合いを定義する
  • ラベル付されていないデータや構造が不明なデータを扱うことになる
  • 目的変数や報酬関数がなくても、データの構造を調べて意味のある構造を取り出すことができる

クラスタリング(clustering)

  • 大量の情報を意味のあるグループ(クラスタ)として構造化できる探索的データ解析手法
  • 教師なし分類(unsupervised　classification)とも呼ぼれる
  • 例として、マーケティング担当者が顧客の関心に基づいて顧客集団を発見できる

データ圧縮のための次元削減

  • 次元削減(dimensionally reduction / dimension resuction)というサブフィールド
  • 教師なし次元削減は特徴量の前処理においてよく使用されるアプローチの一つ

機械学習システム構築

1.前処理：データ整形

  • 生データが機械学習アルゴリズム性能最適化に適した形で提供されることはまずないため、データ前処理((preprocessing)が最も重要な処理の一つとなる

2.予測モデルの訓練と選択

  • 交差検証(cross-validation)では、モデルの汎化性能(generalization　performance)を想定するために、データセットを訓練用と検証用に分割する
  • ハイパーパラメータ最適化(hypeparameter　optimization)はデータから学習されるものではなく、モデルの「ツマミ」を回すのに相当し、回すことでモデルの性能を向上させることができる

3.モデルの評価と未知のインスタンスの予測

  • 訓練データセットにうまく適合するモデルを選択した後は、いわゆる汎化誤差(学習時に使わなかったデータに対する予測値と正解の差)を評価できる
  • 性能に納得がいけば、このモデルを使って将来データを予測できる

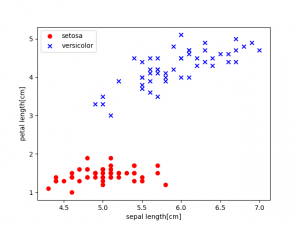
分類問題

  • 散布図

Perceptron01.png

線形分類器

  • 特徴の線形結合の値に基づいて分類を行う確率的分類器である。機械学習において、分類は項目群を特徴値に基づいてグループに分類することを目的とする
  • パーセプトロンアルゴリズムは、完全な線形分類が不可能なデータセットでは決して収束しないため、一般に実務データ解析で推奨されない

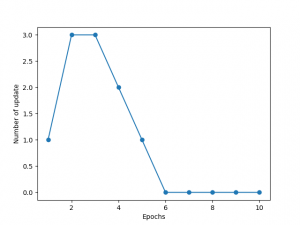
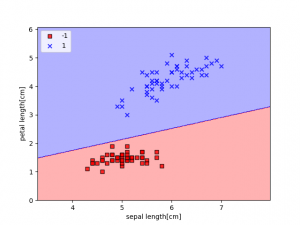
パーセプトロン

パーセプトロンモデルは、脳内の1つのニューロンの働き、発火するかしないか、を模倣

  1. 　重みを0または値の小さな乱数で初期化
  2. 　訓練データごとに次の手順を実行
    1. 　出力値を計算
    2. 　重みを更新

Perceptron02.png Perceptron03.png

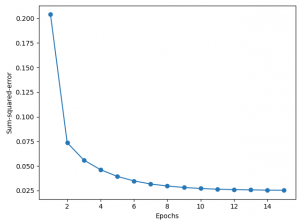
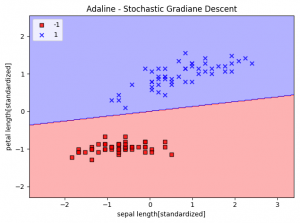
ADALINE

  • パーセプトロンアルゴリズムの改良と見なすことができる。違いは重みの更新方法にある。
  • パーセプトロンのような単位ステップ関数ではなく、線形活性化関数に基づいて重みを更新する

Adaline02.png Adaline01.png

ロジスティック回帰(logistic regression)

  • 線形分類問題と二値分類問題に対する単純ながら強力なアルゴリズムの一つ
  • 名前とは裏腹に怪奇ではなく分類のためのモデル
  • 非常に実装しやすく、線形分離可能なクラスでは非常に性能が良い
  • 産業界において最も広く使われている分類アルゴリズムの1つ

オッズ比

  • 確率[math]\displaystyle{ p }[/math]の場合、事象の起こりやすさをオッズ比（odds ratio)として、[math]\displaystyle{ \tfrac{p}{(1-p)} }[/math]と書くことができる
  • [math]\displaystyle{ p }[/math]は、正事象(positive event 予測したい事象)を表す
  • オッズの対数を取ったものを、ロジット(logit)関数という。

[math]\displaystyle{ logit(p) = log\frac{p}{(1 - p)} }[/math]

  • ロジット関数の逆関数は、ロジスティックシグモイド(logistic sigmoid)関数とも呼ばれる。

[math]\displaystyle{ \phi(z) = \frac{1}{(1 + e^{-z})} }[/math]

scikit-learn

インストール

$ pip install scikit-learn
  • Irisデータセットは、scikit-learnに組み込まれている
>>> from sklearn import datasets
>>> import numpy as np
>>> iris = datasets.load_iris()
>>> X = iris.data[:, [2,3]]
>>> y = iris.target
>>> print('Class labels:', np.unique(y))
Class labels: [0 1 2]

・・・・・・・・・・・・・・・・・

基礎

  • 未定義の値はパラメータ、説明はモデル
  • 典型的には、学習と推論の2段階でアルゴリズムを調べる
  • 学習段階での目的は、特徴モデルと呼ばれるデータを記述し、モデルに要約すること
  • 特徴ベクトルは、実際のデータを単純化したもの、学習・推論のステップはデータそのものではなく、特徴ベクトルに依存
  • 測定する値とどの測定値を比較すべきかの設計は、特徴量設計と呼ばれる
  • 調べる特徴の数が多すぎるとパフォーマンスが低下する可能性(次元の呪い)
  • 同一性は構成されている特徴に分解される

学習アプローチ

  1. 訓練データ
  2. 特徴ベクトル
  3. 学習アルゴリズム
  4. モデル

推論アプローチ

  1. テストデータ
  2. 特徴ベクトル
  3. モデル
  4. 予測

距離の測定

学習のタイプ

教師あり学習
  • モデルと呼ばれるラベル付きデータを必要とする
  • 訓練データセットと呼ばれる例の集まりを使用する
教師なし学習
  • 対応するラベルなしでデータをモデリングする
  • 十分なデータがあれば、パターンや構造を発見できる
  • クラスタリングと次元削減が強力なツールとなる
強化学習
  • 環境が行動によりどう反応するかを観察することで収集される情報を訓練する
  • どのような行動の組み合わせが最も有利な結果をもたらすかを知るため

アルゴリズム

アルゴリズム 用途 備考
線形回帰 トレンドの予測
ロジスティクス回帰 データを2つのカテゴリに分類し、データセットを分割する最善の方法を見つける
多クラスタロジスティクス回帰 データを複数のカテゴリに分類する
隠れマルコフモデル(ビタビ) 最も可能性の高い隠れた理由を見出す
k平均法 固定数のカテゴリにクラスタリングし、自動的に分割
自己組織化マップ 任意のカテゴリにクラスタリングし、高次元データを2次元平面上へ非線形写像する
オートエンコーダ 入力されたデータを一度圧縮し、重要な特徴量だけを残した後、再度もとの次元に復元
Qポリシーニューラルネットワーク ニューラルネットワークを用いた環境での強化学習
パーセプトロン 教師ありニューラルネットワークを用いたデータの分類
畳み込みニューラルネットワーク 教師ありニューラルネットワークを用いた次世界画像の分類
リカレントニューラルネットワーク ニューラルネットワークを使用して観測に一致するパターンを生成
シーエンス変換(Seq2seq)モデル 自然言語の問い合わせに対する自然言語応答の予測
順位付け 効用の学習によって項目を順位付けするための学習

線形回帰

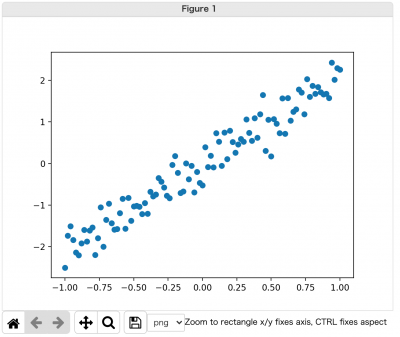
バリアンスとバイアス

  • バイアスとバリアンス（偏りと分散）のトレードオフ（Bias-Variance Tradeoff）とは？
  • バイアス（偏り：Bias）とは、予測値と真の値（＝正解値）とのズレ（つまり「偏り誤差：Bias error」）を指す
    • バイアス（偏り誤差）が大きすぎる場合、そのモデルは入力と出力の関係性を正確に表現できていない（＝訓練データでさえも正確に予測できない）といえる。いわゆる「学習不足（＝過少適合：under-fitting）」の状態
  • バリアンス（分散：Variance）とは、予測値の広がり（つまり「ばらつき誤差：Variance error」）を指す。この予測誤差は、訓練データの揺らぎから生じる
    • バリアンス（ばらつき誤差）が大きすぎる場合、そのモデルは訓練データのノイズまで学習してしまっている（＝テストデータなど未知のデータでは正確に予測できない）。いわゆる「過学習（＝過剰適合：over-fitting）」の状態

TensorFlow 

import matplotlib
matplotlib.use("WebAgg")
import numpy as np
import matplotlib.pyplot as plt

x_train = np.linspace(-1, 1, 101)
y_train = 2 * x_train + np.random.randn(*x_train.shape) * 0.33

plt.scatter(x_train, y_train)
plt.show()

Ml regression.png

TensorFlow


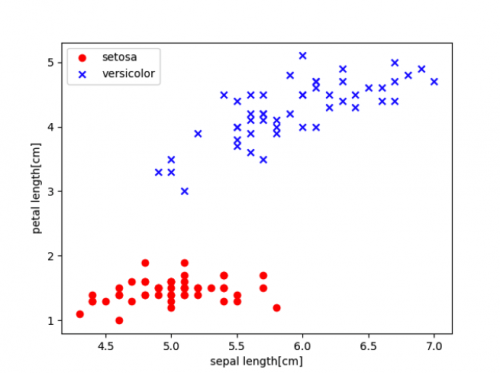
Irisデータセット

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
df = pd.read_csv(url, header=None, encoding='utf-8')
result = df.tail()
print(result)

y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-secosa', -1, 1)
X = df.iloc[0:100, [0, 2]].values
plt.scatter(X[:50,0], X[:50,1], color='red', marker='o', label='setosa')
plt.scatter(X[50:100,0], X[50:100, 1], color='blue', marker='x', label='versicolor')
plt.xlabel('sepal length[cm]')
plt.ylabel('petal length[cm]')
plt.legend(loc='upper left')
plt.savefig('03.sample.png') # 画像を保存
plt.show()

Iris df01.png

「https://www.typea.info/tips_/index.php?title=機械学習&oldid=33518」から取得

© 2006 矢木浩人